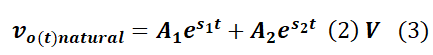Objetivo del taller: Simular el comportamiento del circuito eléctrico de la figura 1 utilizando la herramienta de Matlab Simulink:
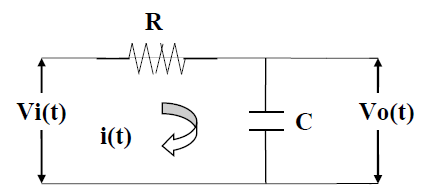
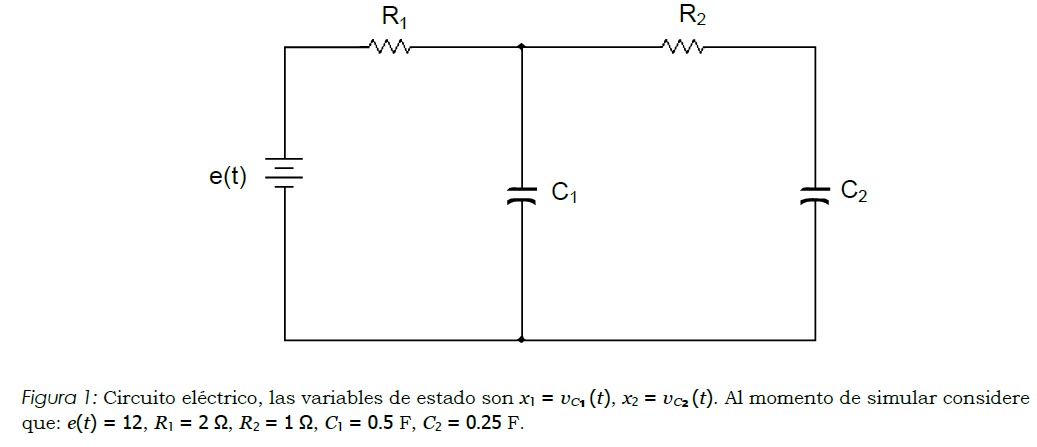
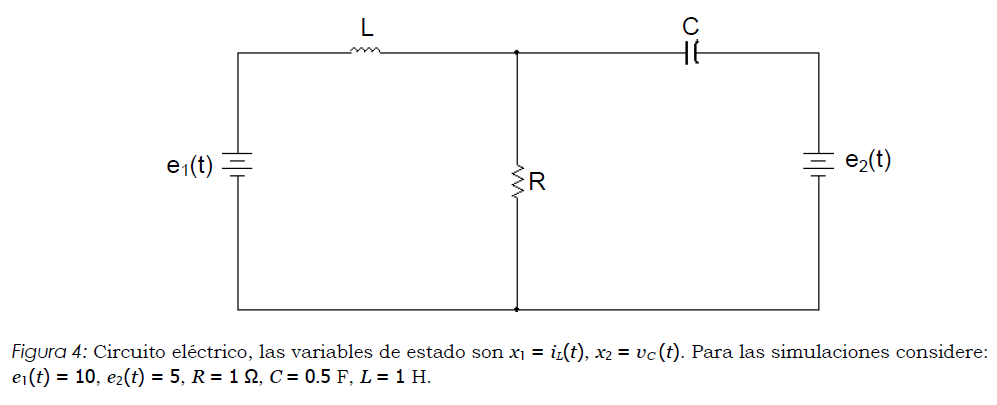
Figura 1
Considerar para los componentes los valores que se indican a continuación:

Para cada uno de los circuitos (casos a y b) llevar a cabo las siguientes acciones:
- Obtener la función de transferencia.
- Realizar un diagrama de bloques en Simulink y obtener la respuesta del circuito a una entrada escalón (step)
- Puesto que son sistemas muy rápidos, para realizar la simulación hay que cambiar los valores que Simulink usa por defecto: simular durante 0.05 s en el caso a) y 0.005 s en el caso b).
- No olvidar poner el comienzo del escalón unitario en el instante t=0 (doble click sobre el bloque ‘step’ una vez situado en la ventana en la que estamos haciendo el modelo y cambir ‘step time’ a 0)
- Calcular sobre la gráfica obtenida en el osciloscopio la constante de tiempo del sistema, la ganancia estática y su tiempo de establecimiento.
- Verificar analíticamente los resultados obtenidos en la simulación, es decir, compararlos con los valores que se obtienen al hacer los cálculos matemáticos.
- ¿Qué relación hay entre el valor de la constante de tiempo y la velocidad de respuesta del sistema?
- Cambiar la entrada y obtener la respuesta del circuito a una entrada rampa unitaria (ramp).
- Medir el error en el estado estacionario para los dos circuitos. ¿Qué relación hay entre el valor medido y la constante de tiempo de cada sistema?
Respuesta
- Obtener la función de transferencia
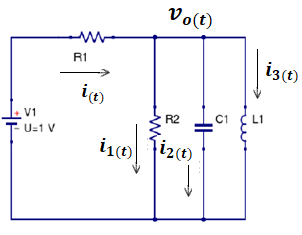
Aplicando la ley de voltajes de Kirchhoff al circuito de la figura 1 obtenemos la siguiente relación:
Suponiendo condiciones iniciales iguales a cero y aplicando la transformada de Laplace a la ecuación anterior obtenemos: Es decir:
Es decir:
De donde: La salida es vo(t):
La salida es vo(t):
La transformada de Laplace de la salida vo(t) es:
De donde obtenemos la función de trasferencia del sistema:

En el caso del sistema a):



En el caso del sistema b):



- Realizar un diagrama de bloques en Simulink y obtener la respuesta del circuito a una entrada escalón (step)
El siguiente diagrama de bloques representa en general a un sistema de primer orden como lo es la función de transferencia del sistema de la figura 1:

Figura 2
En el diagrama de bloques de la figura 2, la variable T es la constante de tiempo del sistema. En el caso del sistema de figura 1, la contante de tiempo del sistema es:
Sistema a):

Sistema b):

Simulación en Simulink
En Simulink corremos la simulación para el sistema general de la Figura 2 para una entrada escalón unitario y T=1 s, y obtenemos: 
Figura 3
En la gráfica 1 el tiempo está representado por el eje de las abscisas mientras la amplitud de la salida está representada en el eje de las ordenadas. Y en una gráfica más amplia de la pantalla del scope (Figura 4) podemos ver que la salida sigue a la entrada en estado estable, es decir, su valor final es uno, mientras que en t=T=1 s, la respuesta del sistema ha alcanzado alrededor del 63,2% de su valor final, es decir, 0.633, como lo señala la definición teórica de constante de tiempo de un sistema de primer orden.

Gráfica 1
Hacemos la simulación para los sistemas a) y b):
Sistema a):


 Gráfica 2
Gráfica 2
La gráfica 2 muestra la forma de la curva para el voltaje de salida del sistema de la figura 1, típica respuesta para un sistema RC en serie, donde se espera que el voltaje en el capacitor sea cero en t=0 s, para luego aumentar exponencialmente hasta igualarse en valor al voltaje de entrada (vin=1, escalón unitario) cuando ha transcurrido bastante tiempo, es decir, en estado estable, cuando el capacitor se comporta como un circuito abierto.
Sistema b):



Gráfica 3
La gráfica 3 muestra nuevamente la forma de la curva para el voltaje de salida del sistema de la figura 1. La única diferencia con respecto a la respuesta de la gráfica 2 es que el tiempo está multiplicado por un factor 10-4, en vez de 10-3,es decir, el sistema b) es 10 veces más rápido que el sistema a).
- Calcular sobre la gráfica obtenida en el osciloscopio la constante de tiempo del sistema, la ganancia estática y su tiempo de establecimiento.
Sistema a)

Gráfica 4
En la gráfica 4 repetimos la gráfica 2, señalando los parámetros del sistema. La constante de tiempo es T=0.52 ms aproximadamente, mientras que aplicando el criterio del 2% podemos ver que el tiempo de establecimiento es de 2 ms, cuando la salida está a 0.02 puntos de alcanzar su valor final. La ganancia estática es 1.
Sistema b)

Gráfica 5
En la gráfica 5 repetimos la gráfica 3, señalando los parámetros del sistema. La constante de tiempo es T=0.052 ms aproximadamente, mientras que aplicando el criterio del 2% podemos ver que el tiempo de establecimiento es de 0.2 ms, cuando la salida está a 0.02 puntos de alcanzar su valor final. La ganancia estática es 1.
- Verificar analíticamente los resultados obtenidos en la simulación, es decir, compararlos con los valores que se obtienen al hacer los cálculos matemáticos.
Ya habíamos visto que el siguiente diagrama de bloques representa en general a un sistema de primer orden:

Figura 4
La función de transferencia del sistema general de la figura 4 la podemos obtener mediante:

En la ecuación (1), T es la constante de tiempo de un sistema de primer orden. Por otra parte, según el criterio del 2%, el tiempo de establecimiento ts en el caso de un sistema de primer orden es:

Para cada uno de los sistemas estudiados, a continuación se muestra la función de transferencia con la misma forma de la ecuación (1), la constante de tiempo y el tiempo de establecimiento según el criterio del 2%:
Sistema a):

Si comparamos estos resultados con la simulación hecha en Simulink para el sistema a) vemos que se aproximan los valores de ambos resultados:

Sistema b):

Si comparamos estos resultados con la simulación hecha en Simulink para el sistema b) vemos que se aproximan los valores de ambos resultados:

En cuanto a la ganancia estática, se constata que al obtener el límite cuando t tiende a infinito (s tiende a cero) el valor en estado estable de cada sistema es 1, tal cual como se ve en la simulación de cada sistema:

- ¿Qué relación hay entre el valor de la constante de tiempo y la velocidad de respuesta del sistema?
La relación entre valor de la constante de tiempo T y la velocidad de respuesta del sistema es la siguiente:
- Cuando ha pasado un tiempo t=T, el sistema ha alcanzado el 63,2% de su valor final;
- Cuando ha pasado un tiempo t=2T, el sistema ha alcanzado el 86,5% de su valor final;
- Cuando ha pasado un tiempo t=3T, el sistema ha alcanzado el 95% de su valor final;
- Cuando ha pasado un tiempo t=4T, el sistema ha alcanzado el 98.2% de su valor final;
- Cuando ha pasado un tiempo t=5T, el sistema ha alcanzado el 99.3% de su valor final;
Para poner un ejemplo, ubicamos en la gráfica 6, generada por la simulación para el sistema b) , el valor de la salida para t=3T, corroborando que la salida ya ha alcanzado un valor de 0.95 (95% de su valor final):

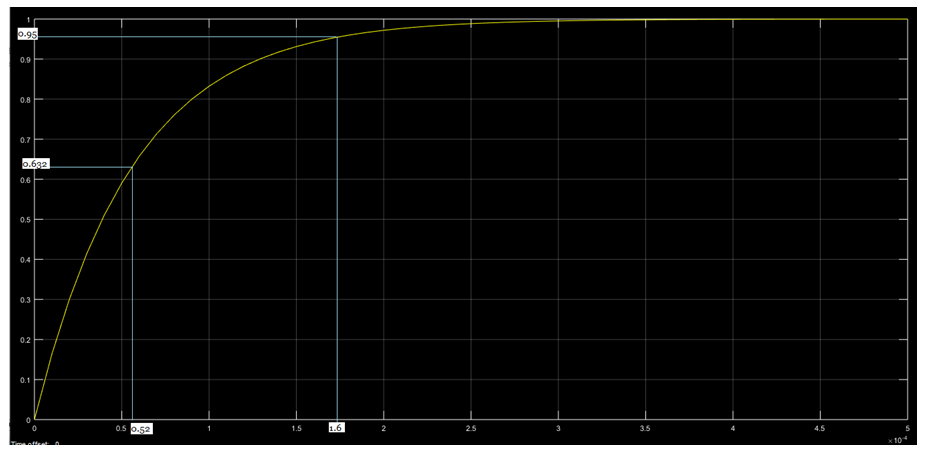
Gráfica 6
También cabe resaltar, como se dijo antes, que el sistema b) es más rápido que el a) porque su constante de tiempo es más pequeña. En conclusión, mientras más pequeña sea la constante de tiempo de un sistema, más rápido es.
- Cambiar la entrada y obtener la respuesta del circuito a una entrada rampa unitaria (ramp).
Sistema a):


Gráfica 7
Sistema b):


Gráfica 8
- Medir el error en el estado estacionario para los dos circuitos. ¿Qué relación hay entre el valor medido y la constante de tiempo de cada sistema?
Por medio de las gráficas 1 y 2 para cada sistema podemos ver que en ambos casos, cuando la entrada es la función escalón unitario, el error en estado estacionario es cero, es decir, el valor de la salida es 1 en estado estacionario, igual al valor de la entrada.
Por otra parte, para visualizar el error en estado estable cuando la entrada es la rampa unitaria, veamos la siguiente gráfica en el caso del sistema a), donde la curva amarilla es la respuesta del sistema y la curva azul es la entrada:

Gráfica 9
En la gráfica 9 podemos ver que después una constante de tiempo, el error en estado estable en el sistema a) es aproximadamente de 0.5×10-3. En cuanto al sistema b) cuya entrada y salida se muestran en la gráfica 10, este error es de 0.5×10-4.

Gráfica 10
Para corroborar estas afirmaciones vamos a calcular el error en estado estable analíticamente.
Para medir el error en estado estacionario utilizamos las constantes de posición y velocidad kp y kv, respectivamente, de cada sistema:
Sistema a):

Se confirma que el error en estado estacionario del sistema a) para la entrada escalón unitario es:

Mientras, el error en estado estacionario del sistema a) para la entrada rampa unitaria es:

Como se puede ver, estos resultados corroboran aquellos obtenidos mediante la gráfica para el sistema a). Igual sucede para el sistema b)
Sistema b):

De acuerdo con estos últimos resultados es clara la relación que existe entre la constante de tiempo y el error en estado estable para la entrada rampa. Ambos valores son iguales.
Siguiente:
Revisión literaria hecha por:
Prof. Larry Francis Obando – Technical Specialist – Educational Content Writer
Se hacen trabajos, se resuelven ejercicios!!
WhatsApp: +34633129287 Atención Inmediata!!
Copywriting, Content Marketing, Tesis, Monografías, Paper Académicos, White Papers (Español – Inglés)
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.
Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV Caracas.
Escuela de Turismo de la Universidad Simón Bolívar, Núcleo Litoral.
Contacto: España. +34633129287
Caracas, Quito, Guayaquil, Cuenca.
WhatsApp: +34633129287
FACEBOOK: DademuchConnection
email: dademuchconnection@gmail.com



el circuito equivalente es el siguiente:











































 La salida es vo(t):
La salida es vo(t):














 Gráfica 2
Gráfica 2










































 La cual tiene las raíces:
La cual tiene las raíces: