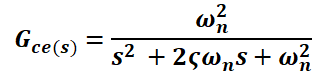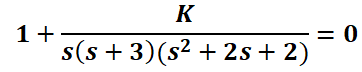Para determinar los valores de las constantes Kp y Td de un controlador PD, utilizaremos Matlab. Considere un Sistema con una planta inestable con función de transferencia Gp(s):

Usando el enfoque del LGR diseñar un control proporcional-derivativo (determinar los valores de Kp y Td) tal que el factor de amortiguamiento relativo ζ del sistema en lazo cerrado sea 0.7 y la frecuencia natural no amortiguada ωn sea 0.5 rad/seg.
Respuesta:
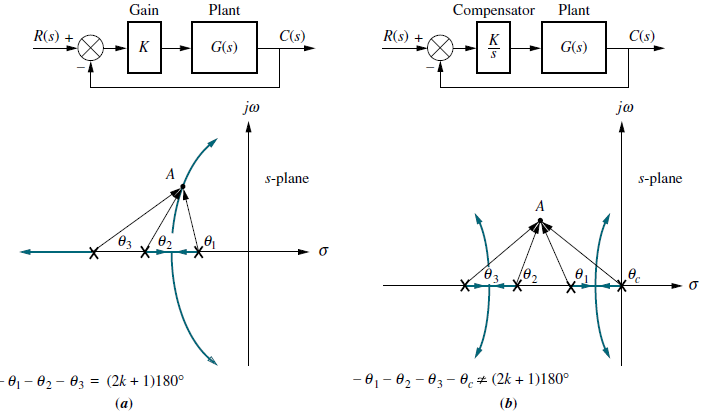
- Para describir cualitativamente el comportamiento de la planta, la incorporamos a un sistema de control elemental (realimentación unitaria) como el que se muestra en el siguiente diagrama de bloques, Figura 1:

Luego, observamos el Lugar Geométrico de sus Raíces (LGR) mediante el siguiente comando en Matlab (para un repaso de LGR ver:):
>> G=tf([1],[10000 0 -11772])
>> rlocus(G)
>> grid

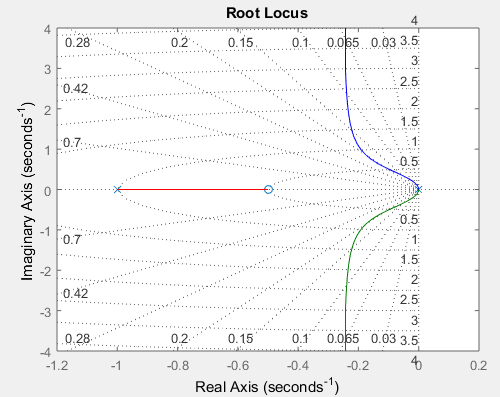
Podemos ver en la Figura 2 que para ganancias cercanas a 1, el sistema tiene raíces ubicadas en el lado derecho del plano s, por lo tanto se trata de un sistema inestable (para un repaso de estabilidad ver:Estabilidad). Podemos además solicitar a Matlab las raíces de nuestra planta para la ganancia exactamente igual a 1 mediante:
>> pole(G)
ans = 1.0850 -1.0850
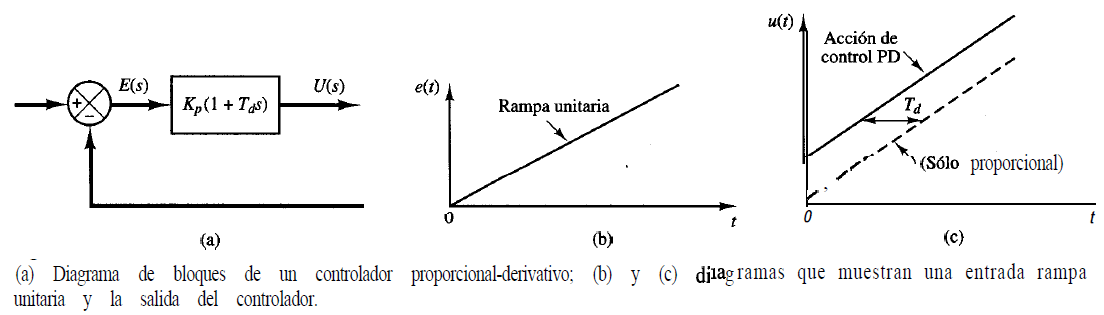
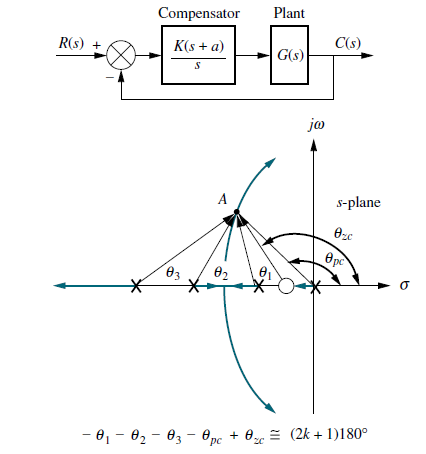
Para alcanzar las especificaciones solicitadas (factor de amortiguamiento ζ=0.7 y frecuencia natural no amortiguada ωn =0.5 rad/seg.), introducimos en la función de transferencia directa un controlador PD, Figura 3:

La justificación de aplicar un controlador PD es que las especificaciones involucran a la respuesta transitoria, etapa en la cual la aplicación del controlador PD es ideal, según se concluye en la teoría. Analíticamente ya se demostró en Controlador PD que los valores de las constantes son Kp =14272 y Td =0.49 s. En esta oportunidad vamos a determinar estos valores utilizando el Matlab Control System Toolbox, en especial el comando sisotool:
>> sisotool(G)
Esta herramienta ofrece una interface gráfica que facilita el diseño del controlador de acuerdo con los requerimientos solicitados (Graphical Tuning, Root Locus Design). En la Figura 4 podemos observar las dos pantallas iniciales:


Figura 4
Hacemos click derecho sobre el LGR, seleccionamos las pestañas según la Figura 5:



Al asignar el valor del parámetro ζ, obtenemos la siguiente gráfica:

Aplicamos el mismo procedimiento para asignar el valor de ωn:



Al asignar los valores solicitados en las ventanas para cada parámetro, obtenemos la siguiente gráfica:

En la Figura 8 el punto donde se interceptan las curvas negras señalan el lugar geométrico donde se cumplen ambas especificaciones.
Como ya sabemos, agregar un controlador PD es agregar un cero y una ganancia (ver Controlador PD). Ello lo podemos hacer utilizando el menú del LGR:

Procedemos agregar un cero al eje real del plano s:

Ahora arrastramos el cero a lo largo del eje real, utilizando click derecho, hasta que el LGR (líneas azules) coincida con el punto de intercepción de las líneas negras:

Ahora, arrastramos los polos hasta el punto de intercepción de las curvas negras y el LGR:

En el borde inferior izquierdo, mientras ubicamos los polos en el lugar correcto del LGR, podemos ver como evolucionan los valores de los parámetros damping y frecuencia natural;

Seleccionamos la pestaña “compensator editor” para ver los cambios en el controlador:

Vemos que los valores del compensador se asemejan a los obtenidos de manera analítica:

En la misma ventana del “compensator editor” seleccionamos la pestaña “Analysis Plots”:


De manera automática obtenemos la gráfica de respuesta del sistema a la entrada escalón unitario:

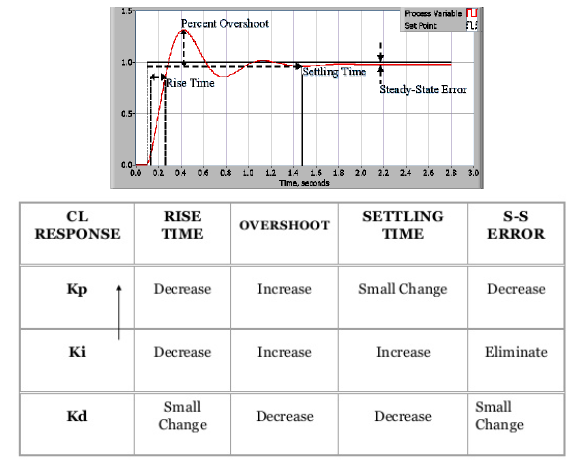
A la gráfica de la Figura 16 se le puede pedir otros valores de importancia en la respuesta transitoria del sistema, como por ejemplo el sobreimpulso:

Otro Ejemplo
Utilice MATLAB y su «Control System Toobox«, y los siguientes pasos y comandos para desarrollar el diseño del pasado ejemplo, por medio de SISOTOOL:
- Escriba sisotool en el MATLAB Command Window.
- Seleccione Import en el File menu de SISO Design para SISO Design Task Window.
- En Data field para G, escriba zpk([],[0,-4,-6],1) y apriete ENTER. Click OK.
- En el Edit menu elija SISO Tool Preferences . . . y seleccione Zero/pole/gain: en el Options tab. Click OK.
- Right-click en el espacio en blanco del LGR y seleccione Design Requirements/New . . .
- Sellecione Percent overshoot y escriba 16. Click OK.
- Right-click en el espacio en blanco del LGR y seleccione Design Requirements/New . . .
- Elija Settling time y click OK.
- Arrastre la linea vertical de settling time hasta interceptar el LGR con la linea radial equivalente a 16% de overshoot.
- Lea el settling time en la parte inferior de la ventana.
- Arrastre la linea vertical de settling time hasta el tiempo equivalente al 1/3 del valor determinado en el paso 9.
- Click en red zero icon en la barra del menú. Coloque el zero en el eje real del LGR con un clicking-again en el eje real.
- Left-click en el eje real zero y arrastrelo a lo largo del eje real hasta que el LGR intercepte el settling time y la linea del percent overshoot .
- Arrastre un cuadro rojo a lo largo del LGR hasta que el cuadro esté en intersección con la línea de settling time, y la línea de percent overshoot.
- Click el Compensator Editor tab de la ventana de Control and Estimation Tools Manager para ver los valores del compensador que arroja el sistema como resulatdo del diseño, incluyendo el valor de la ganancia.
Entradas Relacionadas:
- Efecto de añadir un Zero – Diseño de Sistema de control (English version)
- Controlador PD – Proporcional Diferencial – Sistemas de Control (English version)
- Simulación de Respuesta Transitoria con Matlab
- Respuesta transitoria de un sistema de control Prototipo
- Respuesta Transitoria de un Sistema de Control
- Ejemplo 1 – Respuesta transitoria de un sistema electromecánico
- Análisis de respuesta transitoria – Problemas resueltos – Catálogo 9
Fuente:
- Ingeniería de Control Moderno 3ra. Ed. Katsuhiro Ogata.
- Control Systems Engineering, Nise
- 4 PD, PI, PID
Revisión literaria hecha por:
Prof. Larry Francis Obando – Technical Specialist – Educational Content Writer
Se hacen trabajos, se resuelven ejercicios!!
WhatsApp: +34633129287 Atención Inmediata!!
Copywriting, Content Marketing, Tesis, Monografías, Paper Académicos, White Papers (Español – Inglés)
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.
Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV CCs
Escuela de Turismo de la Universidad Simón Bolívar, Núcleo Litoral.
Contact: Caracas, Quito, Guayaquil, España. telf – +34633129287
WhatsApp: +34633129287
FACEBOOK: DademuchConnection
email: dademuchconnection@gmail.com





















































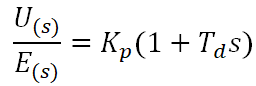 La acción proporcional-derivativa es un caso particular del controlador PID. Las acciones P, I y D están en paralelo (sumas), con una ganancia diferente, tal como se muestra en la Figura 1:
La acción proporcional-derivativa es un caso particular del controlador PID. Las acciones P, I y D están en paralelo (sumas), con una ganancia diferente, tal como se muestra en la Figura 1: