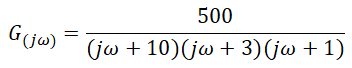Sampling – Chapter One
Sampling with a periodic impulse train.
The Periodic Sampling is the typical method of obtaining a Discrete-time representation of a Continuous-time signal, wherein a sequence of samples x[n] is obtained from a Continuous-time signal xc(t), according to the relation:
Where T is the sampling period and its reciprocal, Fs=1/T, is the sampling frequency. We refer to a system that implements the operation of equation (1) as an ideal continuous-to-discrete-time (C/D) converter.
To derive the frequency-domain relation between the input and output of an ideal C/D converter, first consider the conversion of xc(t) to xs(t) through modulation of the periodic impulse train:
We modulate the periodic impulse s(t) train with xc(t), obtaining:
Through the “sifting property” of the impulse function, xs(t) can be expressed as:
Figure 4.2(a) is strictly a mathematical representation that is convenient for gaining insight into sampling in both time domain and frequency domain. It is not a close representation of any physical circuit or system. This representation leads to a simple derivation of a key result and to a number of important insights that are difficult to obtain from a forma derivation based on manipulation of Fourier Transform formulas.
The sampling operation is generally not invertible; i.e., given the output x[n], it is not possible to reconstruct xc(t), the input to the sampler, since many continuous-time signals can produce the same output sequence. The inherent ambiguity in sampling is a fundamental issue in signal processing. Fortunately, it is possible to remove the ambiguity by restricting the input signals that go into the sampler.
Figure 4.2 (b) shows a continuous-time signal xc(t) and the results of impulse train sampling for two different sampling rates. Figure 4.2 (c) depicts the corresponding output sequences. The essential difference between xs(t) and x[n] is that xs(t) is, in a sense, a continuous-time signal that is zero except at integer multiples of T. The sequence x[n], on the other hand, is indexed on the integer variable n, which in effect introduces a time normalization; i.e., the sequence of numbers x[n] contains no explicit information about the sampling rate. Furthermore, the samples of xc(t) are represented by finite numbers in x[n] rather than as an area of impulses, as with xs(t).
Sampling principle.
A band-limited signal xc(t) with bandwidth Fo can be reconstructed from its sample values x[n]=xc(nT), if the sample frequency Fs=1/Ts is greater than twice the bandwidth Fo of xc(t):
Otherwise, aliasing would result in x[n]. The sampling rate of 2Fo for an analog band-limited signal is called the Nyquist rate.
Note: according to Nyquist criteria, after xc(t) is sampled, the highest analog frequency that x[n] represents must be Fs/2 (i.e. ω=π).
Band-limited signal.
A continuous-time signal xa(t) is band-limited if there exist a finite radian frequency Ωo such that the CT-Fourier Transform Xa(jΩ) is zero for |Ω|> Ωo:
The frequency Fo is called the signal bandwidth in Hz.
Aliasing.
Let xa(t) be an analog (absolutely integrable) signal. The continuous-time Fourier Transform (CTFT) of xa(t) is:
Meanwhile:
In consequence, it can be shown that the discrete-time Fourier Transform (DTFT) of x[n] is a countable sum of amplitude-scaled, frequency-scaled, and translated version of the Fourier Transform Xa(jΩ):
This relation is known as the aliasing formula. The analog and digital frequencies are related through Ts:
While the sampling frequency Fs is given by:
When we want to express the sampling frequency in radians per second, we also use:
The graphical illustration of the aliasing phenomena is given by Figure 3.10:
Combining this we obtain this simple aliasing principle:
Example 3.17
The analog signal xa(t) is sampled at Fs to obtain the discrete-time signal x[n]. Determine x[n] and its corresponding DTFT.
Solution:
First, we must identify the highest frequency in xa(t). That will be F0:
Since Fs <2 F0, there will be aliasing in x[n] after sampling. i.e., we will get the following case:
The sampling interval is:
Hence, we have:
That is:
Note that the highest digital frequency of x[n] is 1.75π, which is outside the Nyquist interval –π<ω<π, signifying that aliasing will occur. From the periodicity property of digital sinusoidal sequences, we know that x[n] will be repeated every 2π. So, the alias of x[n] can be determined by:
Using Euler’s identity:
From table 3.1 and the DTFT properties, the DTFT of x[n] is:
The plot of X(ejω) is shown in Figure 3.15.
Source:
Ingel V.; Proakis J. Digital Signal processing using Matlab (p 81)
Oppenheim A.; Schafer R.; Buck J. Discrete Time Signal Processing (p 141)
Book Review by Larry Obando – Electrical Engineering –
Universidad Simón Bolívar – Universidad Central de Venezuela
Mathematical Modeling and Simulation Services – whatsapp +34633129287
la parte real se vuelve negativa. En 
, el diagrama de Nyquist cruza el eje real negativo ya que el término imaginario va a cero. El valor real en el cruce del eje, punto Q’ en la Figura 4 (c), es -0.874. Continuando hacia, la parte real es negativa, y la parte imaginaria es positiva. A frecuencia infinita:
dademuchconnection 