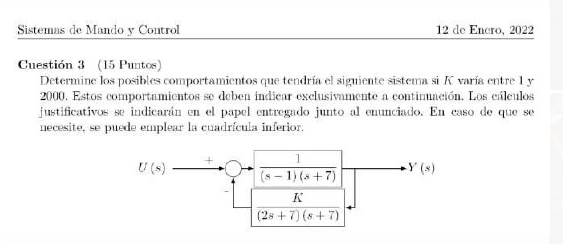
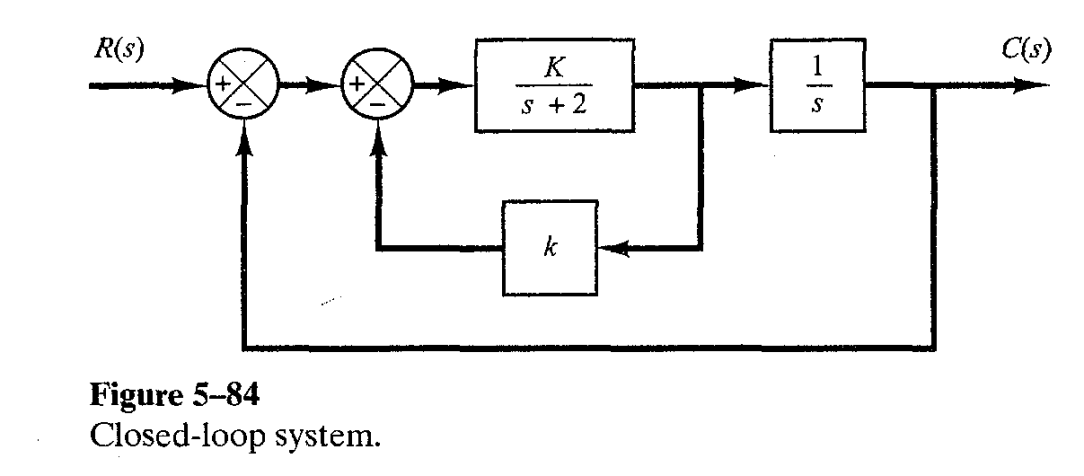
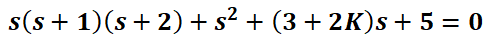To better appreciate the effect of the PD controller, let’s look at the following example. Suppose we have the system of Figure 7-23.

The direct transfer function G(s) for this system is as follows:
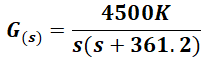
Where K is the pre-amplifier constant.
Teh design specifications for this system are:
 Where:
Where:
- ess: steady-state error for a ramp input
- Mp: Maximum Overshoot
- Tr: Rise time
- Ts: settling time
- Selection of K
The first thing we are going to do is to find out K to meet the first design requirement, ess:![]()
1.a Find the speed constant Kv:
1.b Determine ess as a function of K:
1.c Get K:
With the value of K, the direct transfer function G(s) is: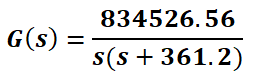
2. Overshoot
2.a The closed-loop transfer function Gce(s) is:

2.b From here we find the damping ζ and the natural frequency ωn.

2.c Determine Mp:
![]() This value exceeds the requirement of the specification, so it is considered to insert a PD controller in the direct path of the system in order to improve the damping and adjust the maximum overshoot to the required design specification, maintaining however the error in state stable at 0.000433.
This value exceeds the requirement of the specification, so it is considered to insert a PD controller in the direct path of the system in order to improve the damping and adjust the maximum overshoot to the required design specification, maintaining however the error in state stable at 0.000433.
3. Design of the PD controller in time domain
From Figure 10-3


and K=185.4503, the direct transfer function G(s) is:

While, the closed-loop transfer function Gce(s) is:

This last equation shows the effects of the PD controller on the closed loop transfer function of the system to which it is applied:
- Add a zero in s=-Kp/Kd
- Increase the «term associated with damping», from 361.2 to 361.2 + 834526.56Kd
3.a Selection of Kp
To ensure that the error is maintained in steady-state for a ramp input according to the specifications, we evaluate that error and select a value for Kp:

When choosing Kp equal to one, we keep the same value for Kv that we had before adding the controller. That is, we keep the error value in steady-state for a ramp input as required by the design specification. So:
 3.b Selection of Kd
3.b Selection of Kd
According to the equation for maximum overshoot: the maximum overshoot depends on the damping ζ. The characteristic equation of the system is:
the maximum overshoot depends on the damping ζ. The characteristic equation of the system is: Where:
Where: We deduce the expression for the damping factor ζ:
We deduce the expression for the damping factor ζ:
 This result clearly shows the positive effect of Kd on the damping. However, it should be noted that the direct transfer function G (s) no longer represents a second-order prototype system, so the transient response will also be affected by zero in s=-Kp/Kd.
This result clearly shows the positive effect of Kd on the damping. However, it should be noted that the direct transfer function G (s) no longer represents a second-order prototype system, so the transient response will also be affected by zero in s=-Kp/Kd.
We will now apply the root locus method to the characteristic equation to examine the effect of varying Kd, while keeping the value of Kp = 1.
If we want to obtain an Mp = 5% as requested in the design specifications, that means obtaining a damping factor equal to the following:


The characteristic equation and its form 1+G(s)H(s) are:
Using the following command in Matlab we obtain the locus of the roots for G(s)H(s):
>> s=tf(‘s’)
>> sys=(834526.56*s)/(s^2+361.2*s+834526.56)
>> rlocus(sys)

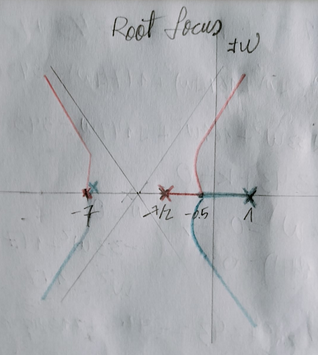
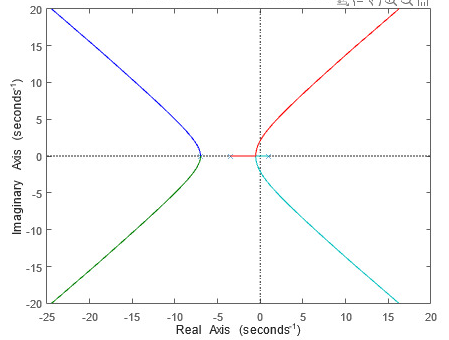
The following graph shows how the damping factor ζ improves as the gain Kd increases:

Meanwhile, the following graph shows that to achieve a damping factor ζ = 0.69 or better than that, which means an overshoot of less than 5% as specified, it is necessary to have a minimum value for the gain Kd= 0.00108:

However, before selecting a final value for Kd, we must observe compliance with the other design requirements.
3.c Evaluation 0f Tr and Ts according to the calculated values for Kd and Kp.
We then analyze the value of the rise time Tr for the value of ζ = 0.69, Kd = 0.00108 and Kp = 1, using the closed-loop transfer function and the graph generated by a step input in Matlab:
>> s=tf(‘s’)
>>sys=(834526.56*(1+0.00108*s))/(s^2+(361.2+834526.56*0.00108)*s+834526.56)
sys = (901.3 s + 8.345e05) / (s^2 + 1262 s + 8.345e05)
> step(sys)

To find Tr, we subtract the times for which C(t)=0.9 y C(t)=0.1:

The previous graph allows us to determine the value of Tr for a value of ζ = 0.69 in the following way:

We can see that this value complies with the requirement of Tr≤0.005 s. Let’s see what happens with Ts. Using 2% criteria:
We can see that the value of the damping ζ = 0.69 does not meet the condition of a Ts less than or equal to 0.005 s, but we can get it by increasing Kd. To be more specific, we clear ζ from the maximum accepted value for Ts:

We use again the locus of the roots to determine what value of Kd corresponds to that of ζ = 0.8757:

If the value of Kd=0.00148 and we keep Kp=1, the direct transfer funcion of the flight system is:
Meanwhile, the closed-loop transfer function of the system under study is the following:

For this transfer function we review the values of maximum overshoot Mp and rise time Tr to ensure that they meet the design specifications:



So, the value for Kd is at minimum:
![]()
And the PD controller can has the following transfer funtion:

Using the following Matlab command, we now proceed to graph the system response before and after adding the PD controller:
>> s=tf(‘s’)
>> G1=(834526.56)/(s*(s+361.2))
>>sys1=feedback(G1,1)
>> G2=(834526.56*(1+0.00148*s))/(s*(s+361.2))
>> sys2=feedback(G2,1)
>> step(sys1,sys2)

In the previous graph the response to the step before placing the PD controller is represented by the blue curve, while the same response after placing the controller is in red. The improvement of the damping is seen since the maximum overshoot is markedly reduced and the rise time is improved.
Made by: Larry Francis Obando – Technical Specialist – Educational Content Writer.
Mentoring Académico / Empresarial / Emprendedores
Copywriting, Content Marketing, Tesis, Monografías, Paper Académicos, White Papers (Español – Inglés)
Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, Caracas.
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, Valle de Sartenejas.
Escuela de Turismo de la Universidad Simón Bolívar, Núcleo Litoral.
Contact: Caracas, Quito, Guayaquil, Cuenca – Telf. 00593998524011
WhatsApp: +593981478463
+593998524011
email: dademuchconnection@gmail.com

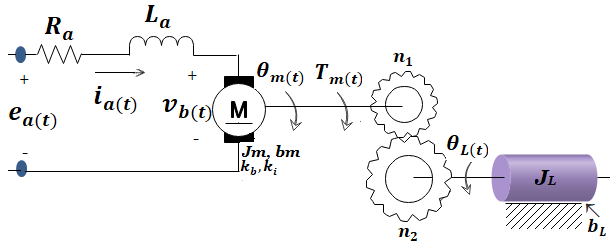



 Figura 3. Motor DC a lazo abierto. a) Esquema general; b) Diagrama de bloques.
Figura 3. Motor DC a lazo abierto. a) Esquema general; b) Diagrama de bloques.




















 Dónde:
Dónde:










 That is to say:
That is to say:










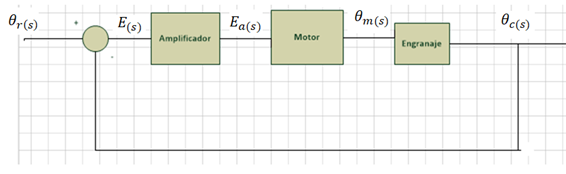
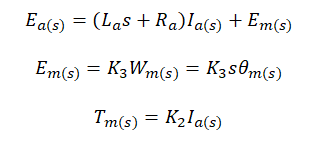 We obtain the following:
We obtain the following: Then, using:
Then, using:



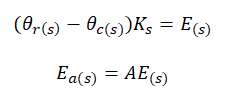

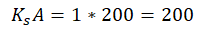


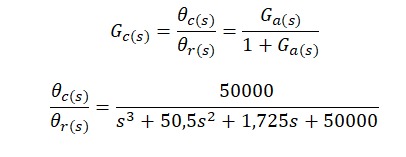


















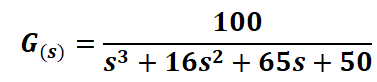













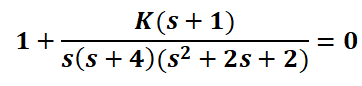














 De esta se obtiene que:
De esta se obtiene que: Luego:
Luego: Es decir:
Es decir: