Concepto de sistema dinámico.
Lo primero que hay que entender sobre los sistemas de control es que son sistemas dinámicos. Según Ogata (1987), autor de uno de los libros más utilizados en las escuelas de ingeniería de control, un sistema es dinámico cuando su salida en el presente depende de una entrada en el pasado. La otra opción es cuando la salida presente del sistema depende sólo de una entrada en el presente, en cuyo caso el sistema se hace llamar estático. Cuando un sistema dinámico no está en su estado de equilibrio, la salida cambia con el tiempo. Mientras, en un sistema estático, la salida permanece constante si la entrada no cambia; es decir, la salida sólo cambia si cambia su entrada. Una breve introducción es ejecutada por el profesor Pedro Albertos de la UPV en el link: Systems and Signals Examples.
Las Figuras 1 y 2 son ejemplos de sistemas estáticos y dinámicos respectivamente. La primera muestra la relación de balance en una palanca apoyada sobre un fulcro (punto de apoyo). El valor presente de la salida y(t) depende del valor presente de la entrada u(t). La segunda muestra que la velocidad y posición de un vehículo depende de una entrada en el pasado.


Los sistemas artificiales tales como la plataforma petrolera de la Figura 3, o la cabina de un avión de la Figura 4, son también ejemplos de sistemas dinámicos de alta complejidad fabricados por los seres humanos:


La respuesta transitoria.
En relación a los sistemas de control, Nise (2011) define un sistema dinámico de la siguiente manera: “A control system is dynamic: It responds to an input by undergoing a transient response before reaching a steady-state response that generally resembles the input” [Nise, 2011, p. 10] (Un sistema de control es dinámico: responde a una entrada por medio de una respuesta transitoria antes de alcanzar una respuesta en estado estable que generalmente sigue, intenta igualar, a la entrada). La Figura 5 muestra un sistema para controlar la posición de una antena. Aquí, la salida es la posición angular (Azimuth Angle), mientras que la entrada es la señal emitida por el potenciómetro. La Figura 6 muestra la salida (línea azul) del sistema mostrado en la Figura 5, en términos de la respuesta transitoria y la respuesta en estado estable, para ambos casos: alta ganancia y baja ganancia.


La intención, la misión del sistema de control de la Figura 5, es colocar la antena en la posición indicada por la entrada, por eso la salida sigue a la entrada. Observando la gráfica de la Figura 6 podemos verificar la característica principal de un sistema dinámico. La entrada o input, se presenta en el tiempo t=0. La respuesta a partir de allí, en cualquier tiempo futuro depende de la entrada en el pasado, o sea, aquella que se presentó en el tiempo t=0. La respuesta transitoria corresponde a aquella que se presenta antes de alcanzar el estado estable, el cual es el valor final de la respuesta del sistema. En la imagen podemos observar dos respuestas transitorias. La primera, de alta ganancia (hig gain), genera alta fluctuación antes de alcanzar el estado estable, pero tiene la ventaja de que es muy rápida en alcanzar el valor final (output), mientras la segunda, de baja ganancia (low gain), presenta poca fluctuación, pero tarda mucho más en alcanzar el valor final. En la primera respuesta podemos imaginar a la antena moviéndose con rapidez súbita y zigzagueando alrededor de su posición final. En el segundo caso, la antena se moverá más lentamente hacia su posición final, a la cual llegará de una manera mucho más amortiguada, serena. La selección de una u otra respuesta dependerá de la necesidad del operador y de los límites de estabilidad del sistema que por lo general se establecen en los requerimientos iniciales.
Sistemas LTI.
Estudiar un sistema de control exige obtener en primer lugar, el modelo matemático de dicho sistema, lo que en realidad implica el desarrollo del modelo de un sistema dinámico.
Un modelo matemático es percibido como un conjunto de ecuaciones que representa la dinámica de un sistema de manera exacta o aproximada. La dinámica de un sistema mecánico, eléctrico o biológico, puede ser representada mediante ecuaciones diferenciales (Ogata, 2002). En general, resolver un problema por lo general requiere en su primera etapa de contar con un modelo sencillo, simplificado, de manera tal que visualizar la solución sea una tarea lo más práctica posible. Para lograr un modelo simplificado, el ingeniero de control debe decidir cuáles de las variables y relaciones físicas son esenciales para el modelo, y cuáles pueden despreciarse (Ogata, 1987). (Por ejemplo, para estudiar el desplazamiento de un resorte que actúa a baja frecuencia, se puede despreciar su masa. Pero, cuando el mismo resorte actúa a alta frecuencia, su masa influye de manera determinante en su desplazamiento, por tanto, no puede despreciarse. De allí a que la ecuación que gobierna el desplazamiento del resorte es más sencilla a baja frecuencia).
Una vez que se tiene una idea aproximada sobre el tipo y la cobertura de la solución, de la conducta y respuesta natural del sistema, el modelo puede ser optimizado, transformándose en uno de mayor complejidad que requiera de la aplicación de software especializado en análisis y simulación, para obtener información oculta en la profundidad de dicha complejidad.
A propósito de la tarea de realizar un modelo, el Prof. del MIT John Sterman comparte su filosofía con nosotros sobre la eficacia de un modelo, mediante las siguientes palabras:
“Every model is a representation of a system…But for a model to be useful, it must address a specific problem and must simplify rather than attempt to mirror an entire system in detail…the usefulness of models lies in the fact that they simplify reality, creating a representation of it we can comprehend…Von Clausewitz famously cautioned that the map is not the territory. It´s a good thing it isn´t: A map as detailed as the territory would be of no use” [Sterman, 2000, p. 89] . (Cada modelo es una representación de un sistema…Pero para que un modelo sea útil, debe enfocarse en un problema específico y debe simplificar en vez de intentar una representación del sistema completo en detalle…la utilidad de los modelos radica en el hecho de que ellos simplifican la realidad, creando una representación de ella que nosotros podamos comprender… Von Clausewitz ofreció su famosa alerta sobre el hecho de que el mapa no es el territorio: Un mapa tan detallado como el territorio sería completamente inútil)
Para obtener las ecuaciones que conforman los modelos de sistemas dinámicos los ingenieros utilizan las leyes de la física, aplicadas a las propiedades de estos sistemas, buscando siempre el camino más fácil para sintetizar el modelo. Entre las propiedades de los sistemas más útiles para alcanzar este objetivo, se encuentran la propiedad de linealidad y la invariancia en el tiempo, básicamente por dos razones principales. En primer lugar, una inmensa cantidad de procesos físicos, sobre todo aquellos que interesan a la ciencia, poseen ambas propiedades. En segundo lugar, los sistemas lineales e invariantes en el tiempo, conocidos también como Sistemas LTI (Linear Time Invariant) son ampliamente accesibles en términos de herramientas disponibles para su análisis. La ciencia de las señales y sistemas ha alcanzado un poderoso desarrollo de estas herramientas, permitiendo que personas de todos los ámbitos académicos puedan aproximarse con facilidad al análisis de los sistemas LTI (Oppenheim, 1996). Es por eso que la comprensión de los sistemas LTI se convierte en la siguiente tarea en la preparación para el análisis de un sistema de control.
Concepto de análisis y diseño.
Antes de profundizar sobre las características de un sistema LTI, es necesario definir las áreas básicas de trabajo del ingeniero de control (Ogata, 1986): el análisis, el diseño y la síntesis de sistemas.
Análisis: es el estudio del funcionamiento de un sistema en condiciones específicas, cuyo modelo matemático se conoce. Por lo general se hacen variar los valores de los parámetros involucrados en los modelos matemáticos para observar las diferentes respuestas y de allí sacar conclusiones. Como el análisis depende del modelo matemático, es independiente del tipo de sistema físico de que se trate, sea este mecánico, eléctrico, hidráulico, etc.
Diseño: dada una tarea específica, se trata del proceso para encontrar el sistema que cumpla con esa tarea. Por lo general no es directo y requiere ensayo y error. El diseño implica por tanto aclarar los requerimientos para el sistema, generalmente dados en términos cuantitativos y cualitativos. Luego, el ingeniero recurre a la síntesis. Una vez dotado de un modelo, mediante simulación computarizada lo analiza para predecir el cumplimiento de los requerimientos. Aplicando ensayo y error, modifica el modelo, hasta aproximarse lo más posible al resultado deseado. De ser posible, fabrica un prototipo y continúa el análisis, hasta cumplir con el objetivo final.
Síntesis: es el uso de un procedimiento explícito para encontrar un sistema que funcione de manera específica. En este caso, las características del sistema se postulan al principio, y luego se utilizan varias técnicas matemáticas para dar con ese sistema.
Existen por tanto, dos métodos de diseño (Distefano et al, 1995):
- Diseño por análisis: hecho por medio de la modificación de las características de un sistema que ya existe;
- Diseño por síntesis: definición de un sistema a partir de sus especificaciones
En relación a los sistemas de control, Nise expone en los siguientes términos las funciones de un ingeniero: “…we discuss three major objectives of systems analysis and design: producing the desired transient response, reducing steady-state error, and achieving stability” [Nise, 2011, p. 10]. (Discutimos tres objetivos principales en el análisis y diseño de sistemas: producir la respuesta transitoria deseada, reducir el error en estado estable y lograr estabilidad).
Caso de aplicación.
Para ilustrar el proceso de obtención de la dinámica de un sistema, utilizaremos el popular del sistema masa-resorte-amortiguador montado en un carro, mostrado en la Figura 7
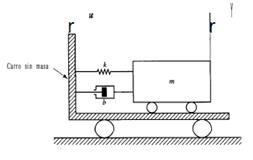
Se supone que el sistema está en reposo en . Lo primero que se debe determinar es cuál es la entrada y cual es la salida del sistema en estudio, a la vez que asignarles un nombre en forma de función dependiente del tiempo, a cada una de ellas. El sistema masa-resorte-amortiguador se moverá en el momento en que el carro se mueve, por lo que el movimiento del carro es la entrada, mientras que el desplazamiento de la masa es la salida. De manera intuitiva podemos prever que si tiene una dirección, digamos a la derecha, entonces tendrá la misma dirección pero con sentido contrario, es decir, a la izquierda.
En el instante el carro se mueve con una velocidad constante, que se representa como la derivada de su desplazamiento con respecto al tiempo, es decir .
El amortiguador actúa como una fricción ante el movimiento de la masa . Dicha masa se desplaza con velocidad . Si la constante del amortiguador de la Figura 7 es , la fuerza que ejerce para oponerse a todo movimiento será proporcional a la velocidad de ese movimiento, en nuestro caso a con pendiente , es decir, estamos ante una función lineal que representa la fuerza de fricción ejercida por el amortiguador al desplazamiento de la masa , y que es igual a . Pero la función ejerce su influencia sobre a través del amortiguador, por lo que tiene un segundo componente que favorece el movimiento de . Dicho desplazamiento es proporcional a y tiene sentido contrario a . De acuerdo con Newton, ambas fuerzas producen una aceleración en la masa que podemos denominar . La relación entre estas fuerzas y dicha aceleración viene dada por la relación formulada por la segunda Ley de Newton: o bien .
El resorte por su parte, también se opone al movimiento de la masa , pero a su vez lo favorece porque el carro también transmite su influencia a la masa a través del resorte. Si la constante del resorte es , y la aceleración de la masa debido al resorte es , la fuerza total que ejerce el resorte sobre la masa es igual a , o bien,
Ahora bien, la expresión matemática que resume la relación entre la aceleración total aplicada sobre la masa , y las fuerzas y , siguiendo la segunda Ley de Newton, es la siguiente:
La ecuación anterior representa la dinámica del sistema, un modelo matemático constituido generalmente por ecuaciones diferenciales como se explicaba en los primeros párrafos de este documento.



