Dinámica de un Sistema Masa-Resorte-Amortiguador

Elementos básicos de un sistema mecánico.

Los elementos básicos de todo sistema mecánico son la masa, el resorte y el amortiguador. El estudio del movimiento en sistemas mecánicos se corresponde con el análisis de sistemas dinámicos. En robótica, por ejemplo, la palabra Forward Dynamic se refiere a lo que le sucede a los actuadores cuando le aplicamos a los mismos ciertas fuerzas y torques.

La masa, el resorte, el amortiguador, son actuadores elementales de un sistema mecánico.

En consecuencia, para controlar el robot es necesario conocer muy bien la naturaleza del movimiento de un sistema masa-resorte-amortiguador.

Además, este sistema elemental se presenta en numerosos campos de aplicación, de allí la importancia de su análisis. De nuevo, en robótica, cuando se habla de Inverse Dynamic, se habla sobre el cómo hacer que el robot se mueva de una manera deseada, cuáles fuerzas y torques debemos aplicar sobre los actuadores para que nuestro robot se mueva de una manera particular.

Atención: Te recomiendo el video siguiente para aprender rápidamente a determinar la Función de Transferencia de un Sistema Masa-Resorte-Amortiguador: https://vm.tiktok.com/ZMLQYbCb6/ Si lo necesitas con urgencia, puedo resolver lo más pronto posible un ejercicio o problema para ti, de Función de Transferencia, Diagrama de Bloques, de un Sistema Mecánico, Eléctrico o Híbrido…comunícate conmigo al whatsapp +34 633129287….costo 13.5 euros pagados por Paypal.

Antes de realizar el Análisis Dinámico de nuestro sistema masa-resorte-amortiguador, debemos obtener su modelo matemático. Éste es el primer paso a ejecutar por toda persona que pretenda conocer a profundidad la dinámica de un sistema, especialmente el comportamiento de sus componentes mecánicos.

Iniciaremos nuestro estudio con el modelo de un sistema masa-resorte.

Esto es conveniente por el motivo siguiente. Todos los sistemas mecánicos presentan una naturaleza en su movimiento que le impulsa a oscilar, como cuando un objeto pende de un hilo en el techo y con la mano lo empujamos. O un zapato sobre una plataforma con resortes. Es bueno saber qué función matemática es la que mejor describe ese movimiento.

Pero resulta que las oscilaciones de nuestro ejemplos no son infinitas. Existe una fuerza de roce que amortigua el movimiento. En el caso del objeto que cuelga de un hilo es el aire, un fluido. Por lo que luego de estudiar el caso de un sistema ideal masa-resorte, sin amortiguación, pasaremos a considerar dicha fuerza de roce y añadir a la función ya encontrada un nuevo factor que describa el decaimiento del movimiento.

 

Sistema Masa-Resorte.

 

Fuente: Física. Robert Resnick

La dinámica de un sistema se representa en primer lugar mediante un modelo matemático compuesto por ecuaciones diferenciales. En el caso de el sistema masa-resorte, dicha ecuación es la siguiente:

Esta ecuación se conoce como Ecuación de Movimiento de un Oscilador Armónico Simple. Veamos de donde se deriva.

Si nuestra intención es obtener una fórmula que describa la fuerza que ejerce un resorte en contra del desplazamiento que lo estira o lo encoge, la mejor manera es visualizando la energía potencial que se inyecta al resorte cuando tratamos de estirarlo o encogerlo. La siguiente gráfica describe cómo se comporta esta energía en función del desplazamiento horizontal:

A medida que la masa m de la figura anterior, sujeta al extremo del resorte como se muestra en la Figura 5, se aleja del punto de relajación del resorte x=0  en sentido positivo o negativo, la energía potencial U(x) se acumula y aumenta en forma parabólica, llegando a un valor superior de energía donde U(x)=E, valor que se corresponde con la máxima elongación o compresión del resorte. La ecuación matemática que en la práctica describe mejor esta forma de curva, incorporando una constante k para la propiedad física del material que aumenta o disminuye la inclinación de dicha curva, es la siguiente:

La fuerza se relaciona con la energía potencial de la siguiente manera:

Por lo tanto:

Tiene sentido ver que F(x) es inversamente proporcional al desplazamiento de la masa m. Porque está claro que si estiramos el resorte, o lo encogemos, esta fuerza se opone a dicha acción, intentando devolver al resorte a su posición relajada o natural. Por ello se le llama fuerza de restitución. La ecuación anterior es conocida en la academia como La Ley de Hooke, o ley de la fuerza para resortes. La siguiente es una gráfica representativa de dicha fuerza, en relación con la energía como se ha venido mencionando, sin intervención de fuerzas de roce (amortiguación), por lo que se le conoce como Oscilador Armónico Simple. Es importante recalcar la relación proporcional entre desplazamiento y fuerza, pero con pendiente negativa, y que, en la práctica, es más compleja, no lineal.

Fuente: Física. Robert Resnick

Para una análisis animado del resorte, corto, sencillo pero contundente, recomiendo observar los videos: Potential Energy of a Spring, Restoring Force of a Spring

AMPLITUDE AND PHASE: SECOND ORDER II (Mathlets)

Amplitude-and-Phase-2nd-Order-II

He realizado un resumen de los textos originales consultados para analizar las ecuaciones de los elementos que se consideran en este documento: masa, resorte, amortiguador.

Regresando a la Figura 5:

Acudimos a la Segunda Ley de Newton:

Esta ecuación nos dice que la sumatoria vectorial de todas las fuerzas que actúan sobre el cuerpo de masa m, es igual al producto del valor de dicha masa por su aceleración adquirida debido a dichas fuerzas. Considerando que en nuestro sistema resorte-masa, ∑F=-kx, y recordando que la aceleración es la segunda derivada del desplazamiento, aplicando la Segunda Ley de Newton obtenemos la siguiente ecuación:

Arreglando un poco las cosas, obtenemos la ecuación que queríamos obtener desde un principio:

Esta ecuación representa La Dinámica de un Sistema Masa-Resorte ideal.

A parte de la Figura 5, otra forma común de representar este sistema es mediante la configuración siguiente:

Fuente: Dinámica de Sistemas. Katsuhiro Ogata

En este caso debemos considerar la influencia del peso en la sumatoria de fuerzas que actúan sobre el cuerpo de masa m. El peso P está determinado por la ecuación P=m.g, donde g es el valor de la aceleración del cuerpo en caída libre.

Si se jala la masa hacia abajo y luego se suelta, actúa la fuerza de restitución del resorte, provocando una aceleración ÿ en el cuerpo de masa m. Obtenemos la siguiente relación aplicando Newton:

Si implícitamente consideramos la deflexión estática, es decir, si realizamos las medidas a partir del nivel de equilibrio de la masa colgando del resorte sin moverse, entonces podemos obviar y descartar la influencia del peso P en la ecuación. Si hacemos y=x, obtenemos de nuevo la ecuación:

Sistema Masa-Resorte-Amortiguador

 

Si no existiera ninguna fuerza de roce, el oscilador armónico simple oscila infinitamente. En la realidad, la amplitud de la oscilación disminuye gradualmente, un proceso conocido como amortiguación, descrito gráficamente a continuación:

Fuente: Física. Robert Resnick

El desplazamiento de un movimiento oscilatorio se grafica contra el tiempo, y su amplitud se representa mediante una función sinusoidal amortiguada por un factor exponencial decreciente que en la gráfica se manifiesta como una envolvente. La fuerza de fricción Fv que actúa en el Movimiento Armónico Amortiguado es proporcional a la velocidad V en la mayoría de los casos de interés científico. Dicha fuerza tiene la forma      Fv = bV, donde b es una constante positiva que depende de las características del fluido que ocasiona la fricción, entre otras cosas. Esta fricción, también conocida como Fricción Viscosa, se representa mediante un diagrama que consiste en un pistón y un cilindro lleno de aceite:

La manera más popular de representar un sistema masa-resorte-amortiguador es mediante una conexión en serie como la siguiente:

Figura 6

Fuente: Física. Robert Resnick

 

Así como la siguiente:

Fuente: Dinámica de Sistemas. Katsuhiro Ogata

En ambos casos se obtiene el mismo resultado al aplicar nuestro método de análisis. Considerando la Figura 6, podemos observar que es la misma configuración mostrada en a Figura 5, pero agregando el efecto del amortiguador. Aplicando la segunda Ley de Newton a este nuevo sistema, obtenemos la siguiente relación:

Esta ecuación representa La Dinámica de un Sistema Masa-Resorte-Amortiguador.

Es de importancia observar que la ecuación (37) es también una Ecuación Diferencial Ordinaria de orden 2 (Ordinary Differential Equation – ODE) porque sólo involucra las derivadas de una sola variable (en este caso x) hasta la segunda derivada. Además, al despejar la ecuación e igualarla a cero, se transforma también en una ODE Lineal Homogénea (Homogeneous Linear ODE) la cual posee importantes propiedades que facilitan el cálculo. Más adelante en este mismo documento veremos eso mediante la aplicación de La Transformada de Laplace. 

Sistema masa-resorte-amortiguador. Problemas resueltos. Catálogo 1

La función de transferencia de un Sistema Masa-Resorte-Amortiguador. 

En esta guía PDF  se determina la Función de Transferencia de los ejercicios que más se utilizan en las clases de sistemas masa-resorte-amortiguador que forman parte a su vez de sistemas de control, señales y sistemas, análisis de redes eléctricas con motor DC, sistemas electrónicos en mecatrónica, etc. Es un buen recurso para aprender también a obtener el diagrama de bloques del sistema, o la representación en variables de estado. Solicitar vía email – WhatsApp. Se facilita pago por PayPal, Tarjeta de crédito o débito. Costo: 21.5 €.

A continuación, los enunciados de problemas resueltos en esta guía (también Resuelvo ejercicios particulares…atención inmediata!!..W+34633129287):

1. La Figura 1 muestra un sistema masa-resorte-amortiguador. La salida es el desplazamiento x_(t) del sistema, mientras que la entrada es la fuerza u_(t) que se ejerce sobre la masa m. Hallar la función de transferencia X_(s)/U_(s).

2. La Figura 2 muestra un sistema masa-resorte-amortiguador montado sobre un carro. El desplazamiento del carro es y_(t) (la entrada) y el desplazamiento del sistema es x_(t) (la salida). Considerar que el carro no tiene masa. Hallar la función de transferencia X_(s)/Y_{(s) .}

3. Hallar la función de transferencia X_2(s)/U_(s) del sistema de la Figura 3 utilizando su modelo en frecuencia y algebra lineal.

4. Hallar la función de transferencia Y_2(s)/U_(s) del sistema de la Figura 4:

5. Hallar la función de transferencia X_2(s)/U_(s) del sistema mostrado en la Figura 5. Ilustrar el uso de diagramas de cuerpo libre.

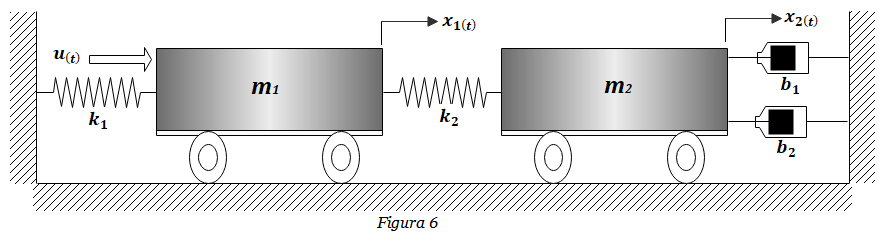
6. Hallar las funciones de transferencia X_1(s)/U_(s), X_2(s)/U_(s), del sistema de la Figura 6.

7. Hallar la función de transferencia X_(s)/U_(s) del sistema presentado en la Figura 7. Comprobar el mismo resultado utilizando la combinación variables de estado – diagrama de bloques. Considerar a x_(t) como la salida y a u_(t) como la entrada.

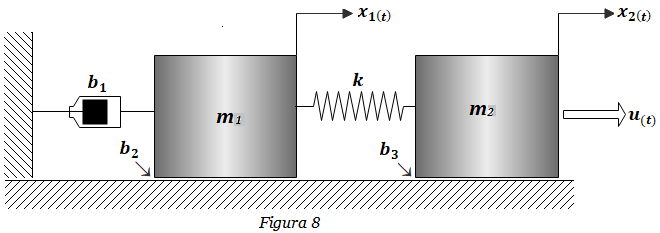
8. Hallar la representación matricial del sistema de la Figura 8. Considere a x_1(t) como la salida, y a u_(t) como la entrada. Construya el diagrama de bloques del sistema y determine la función de transferencia X_1(s)/U_(s).

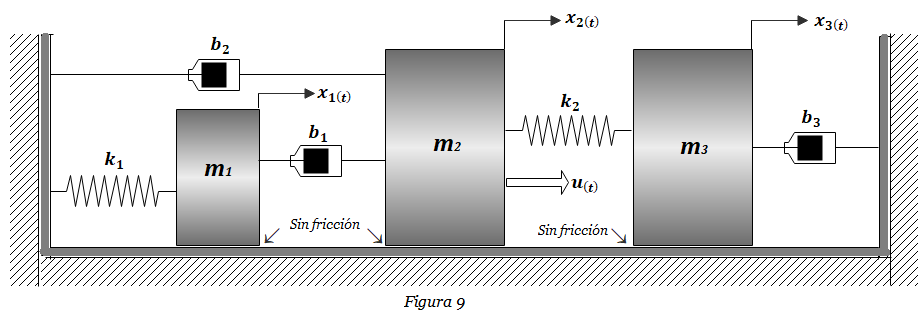
9. Hallar la función de transferencia X_2(s)/U_(s) del sistema mostrado en la Figura 9. Considerar k₁= k₂=6 N/m, b₁= b₂= b₃=2 N-s/m, m₁= m₂= m₃=4 Kg. Ilustrar el uso de Matlab para la aplicación del álgebra lineal.

10. Hallar las funciones de transferencia Y_1(s)/U_(s) y Y_2(s)/U_(s) del Sistema de Suspensión Vehicular de la Figura 10. Considerar k₁= k₂=2 N/m, b=1 N-s/m, m₁= m₂= 2 Kg. (_{El mismo ejercicio se resuelve con variables de estado en el próximo número)}

11. Hallar la representación en el espacio de estados del sistema del ejercicio anterior, Figura 10, considerando u_(t) como la entrada y y_2(t) como la salida. Transformar la representación matricial en la función de transferencia Y_2(s)/U_(s) directamente, utilizando álgebra de matrices. Considerar k₁= k₂=2 N/m, b=1 N-s/m, m₁= m₂= 2 Kg.

 

Sistema masa-resorte-amortiguador. Problemas resueltos. Catálogo 1.

Pago por un solo ejercicio (12.5 euros). Una vez pagado, por favor Solicitar vía whatsapp +34633129287. Ten en cuenta la diferencia horaria. Gracias.

12,50 €

Haz clic aquí para comprar.

Transformada de Laplace de un Sistema Masa-Resorte-Amortiguador

Una solución para la ecuación (37) se presenta a continuación:

Fuente: Física. Robert Resnick

La ecuación (38) muestra claramente lo que se había observado con anterioridad. Un ejemplo puede simularse en Matlab mediante el siguiente procedimiento:

La forma de la curva del desplazamiento en un sistema masa-resorte-amortiguador está representada por una sinusoide amortiguada por un factor exponencial decreciente. Es importante entender que en el caso anterior no se está aplicando ninguna fuerza al sistema, por lo que el comportamiento de este sistema se puede catalogar como «comportamiento natural» (también llamada respuesta homogénea). Más adelante mostramos el ejemplo de aplicar una fuerza al sistema (un escalón unitario), lo que genera un «comportamiento forzado» que influye el comportamiento final del sistema que será el resultado de sumar ambos comportamientos (natural + forzado). Observación: Cuando se aplica una fuerza al sistema, el lado derecho de la ecuación (37) ya no es igual a cero, y la ecuación deja de ser homogénea.

La solución para la ecuación (37) presentada anteriormente, puede derivarse mediante el método tradicional para resolver ecuaciones diferenciales. Sin embargo, dicho método es poco práctico cuando nos encontramos con sistemas más complicados como el siguiente que en los cuáles además se aplica una fuerza f(t):

Figura 7

Fuente: Control System Engineering. Norman Nise.

Surge entonces la propuesta de un método más práctico para hallar la dinámica de los sistemas y facilitar el posterior análisis de su comportamiento mediante simulación computarizada. La Transformada de Laplace permite alcanzar este objetivo de una manera rápida y rigurosa.

En la ecuación (37) no es fácil despejar x(t), que en ese caso es la función de salida y de interés. Tampoco puede representarse una ecuación diferencial en forma de Diagrama de Bloques que es el lenguaje más utilizado por los ingenieros para modelar sistemas, haciendo de lo complejo un objeto visual más fácil de entender y analizar. Esto conduce al primer objetivo para un método más práctico. El primer paso es separar claramente la función de salida x(t), la función de entrada f(t) y la función del sistema, alcanzando una representación como la siguiente:

r(t)=f(t), c(t)=x(t)

Fuente: Control System Engineering. Norman Nise.

La Transformada de Laplace consiste en cambiar las funciones de interés del dominio del tiempo al dominio de la frecuencia mediante la siguiente ecuación:

Fuente: Control System Engineering. Norman Nise.

La ventaja principal de este cambio radica en que transforma derivadas en sumas y restas, luego, mediante asociaciones, podemos despejar la función de interés aplicando las simples reglas del álgebra. Además, no es necesario aplicar la ecuación (2.1) a todas las funciones f(t) que nos encontremos, cuando se dispone de tablas que de antemano ya nos indican la transformada de funciones que se presentan con gran frecuencia en todos los fenómenos, como las sinusoides (salida del sistema masa, resorte y amortiguador) o la función escalón (entrada que representa un cambio brusco). En el caso de nuestros elementos básicos para un sistema mecánico, es decir: masa, resorte y amortiguador, contamos con la siguiente tabla:

Es decir, aplicamos un diagrama de fuerzas para cada unidad de masa del sistema, sustituimos la expresión de cada fuerza en tiempo por su equivalente en frecuencia (que en la tabla se denomina Impedancia, haciendo analogía entre sistemas mecánicos y sistemas eléctricos) y aplicamos la propiedad de superposición (cada movimiento se estudia por separado y luego se suma el resultado).

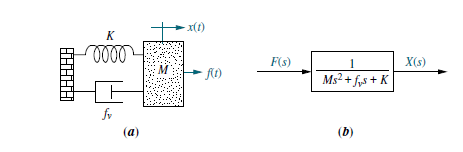
La Figura 2.15 muestra la Función de Transferencia para un sistema masa-resorte-amortiguador cuya dinámica se describe mediante una sola ecuación diferencial:

El sistema de la Figura 7 permite describir un método general bastante práctico para encontrar la función de transferencia de sistemas con varias ecuaciones diferenciales. Primero se aplica el diagrama de fuerzas a cada unidad de masa:

La Transformada de Laplace llama a la función del sistema Función de Transferencia, cuya definición depende de cual es la función de entrada y cual la salida. Por ejemplo, para la Figura 7 nos interesa conocer la Función de Transferencia G(s)=X2(s)/F(s).

Arreglando en forma matricial las ecuaciones del movimiento obtenemos lo siguiente:

Las ecuaciones (2.118a) y (2.118b) muestran un patrón que siempre se cumple y se puede aplicar para cualquier sistema masa-resorte-amortiguador:

La consecuencia inmediata del método anterior es que facilita enormemente obtener las ecuaciones del movimiento para un sistema masa-resorte-amortiguador, al contrario de lo que sucede con las ecuaciones diferenciales. Además, podemos llegar rápidamente a la solución exigida. En el caso de nuestro ejemplo:

donde

que son resultados que se obtienen aplicando las reglas del Algebra Lineal, lo que concede un gran poder computacional al método de Transformada de Laplace.

Ejemplos de aplicación

Ejemplo 1.

Ejercicio B318, Modern_Control_Engineering, Ogata 4t p 149 (162),

Respuesta completa en el siguiente link: Ejemplo 1 – Función Transferencia de Sistema masa-resorte-amortiguador

Ejemplo 2.

1. Control Systems Engineering, Nise, p 101

Respuesta completa en el siguiente link: Ejemplo 2 – Función Transferencia de sistema masa-resorte-amortiguador

Sistema masa-resorte-amortiguador. Problemas resueltos. Catálogo 2

En esta guía PDF  se determina la Función de Transferencia de los ejercicios que más se utilizan en las clases de sistemas masa-resorte-amortiguador que forman parte a su vez de sistemas de control, señales y sistemas, análisis de redes eléctricas con motor DC, sistemas electrónicos en mecatrónica, etc. Solicitar vía email – WhatsApp. Se facilita pago por PayPal, Tarjeta de crédito o débito. Costo por toda la guía: 21.5 €. Costo por un solo ejercicio: 12.5 €.

A continuación, los enunciados de problemas resueltos en esta guía .

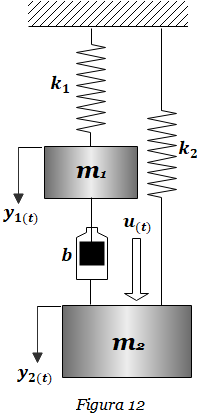
1. Hallar las funciones de transferencia Y_1(s)/U_(s) y Y_2(s)/U_(s) del Sistema que se muestra en la Figura 12.

2. Hallar las funciones de transferencia Y_1(s)/U_(s) y Y_2(s)/U_(s) del Sistema que se muestra en la Figura 13.

3. Hallar las funciones de transferencia X_1(s)/U_(s) y X_2(s)/U_(s) del Sistema mostrado en la Figura 14.

4. Hallar la función de transferencia X_2(s)/U_(s) del Sistema mostrado en la Figura 15. Considerar k₁=1, k₂= 15 N/m, b₁=4, b₂= 16 N-s/m, m₁= 8, m₂=3  Kg.

5. Hallar la función de transferencia X_3(s)/U_(s)  del Sistema mostrado en la Figura 16. Considerar k₁=5, k₂= 4. k₃= 4  N/m, b₁=2, b₂= 2, b₃= 3  N-s/m, m₁= 4, m₂=5, m₃=5  Kg.

6. Hallar la función de transferencia X_1(s)/U_(s) del Sistema mostrado en la Figura 17. Considerar k₁=k₂= 1 N/m, b₁= b₂= b₃= 1  N-s/m, m₁= 2, m₂=1, m₃=1  Kg. _{El mismo ejercicio se resuelve con variables de estado en el próximo número.}

7. Hallar el modelo en espacio de estados del Sistema del ejercicio anterior Figura 17, tomando a x_1(t) como la salida y u_(t) como la entrada. Transformar dicho modelo en la función de transferencia X_1(s)/U_(s). Considerar k₁=k₂= 1 N/m, b₁= b₂= b₃= 1  N-s/m, m₁= 2, m₂=1, m₃=1  Kg.

8. Hallar la función de transferencia Y_h(s)/f_up(s) del Sistema de la Figura 19. Considerar k_h=7, k_s=8, k_ave=5  N/m, b_f=3, b_h= 10  N-s/m, m_h=1, m_f=2 Kg.

9. Hallar las funciones de transferencia X_2(s)/U_(s) y X_3(s)/U_(s) del Sistema de la Figura 20. Considerar k₁=1, k₂=2, k₃=3, k₄=4 N/m, b₁=2,b₂= 1,b₃= 3 N-s/m, m₁=2,m₂=1,m₃=3  Kg.

10. Hallar la representación en espacio de estados tomando x_3(t) como salida y u_(t) como entrada, y la función de transferencia X_3(s)/U_(s) del sistema mostrado en la Figura 21. Considerar k=2 N/m, b₁=b₂=b₃=b₄=b₅=1 N-s/m, m₁=2,m₂=1,m₃=1 Kg.

11. Determinar la función de transferencia y el diagrama de bloques del sistema de la figura 22:

Contacto a través de:

• WhatsApp: +34 633129287
• dademuchconnection@gmail.com

FACEBOOK: DademuchConnection

email: dademuchconnection@gmail.com

Puede pagar a través del siguiente enlace:

Sistema masa-resorte-amortiguador. Problemas resueltos. Catálogo 2.

Pago por toda la guía (21.5 euros). Una vez pagado, por favor Solicitar vía whatsapp +34633129287. Ten en cuenta la diferencia horaria. Gracias.

21,50 €

Click here to purchase.

Sistema masa-resorte-amortiguador. Problemas resueltos. Catálogo 2.

Pago por un solo ejercicio (12.5 euros). Una vez pagado, por favor Solicitar vía whatsapp +34633129287. Ten en cuenta la diferencia horaria. Gracias.

12,50 €

Haz clic aquí para comprar.

Caso Rotacional

Hasta ahora se ha considerado solamente el caso traslacional. En el caso de que el desplazamiento sea rotacional, la siguiente tabla resume la aplicación de la transformada de Laplace en ese caso:

Para ilustrar su uso consideramos el siguiente ejemplo:

Las siguientes figuras ilustran la manera cómo realizar el diagrama de fuerzas para este caso:

De esta manera, el resultado se obtiene a continuación:

Siendo:

Observamos que de nuevo se cumple que:

Sistema masa-resorte-amortiguador. Sistema Rotacional. Problemas resueltos. Catálogo 3

La función de transferencia de un Sistema Masa-Resorte-Amortiguador. 

En esta guía PDF  se determina la Función de Transferencia de los ejercicios que más se utilizan en las clases de sistemas masa-resorte-amortiguador rotacional que forman parte a su vez de sistemas de control, señales y sistemas, análisis de redes eléctricas con motor DC, sistemas electrónicos en mecatrónica, etc. Es un buen recurso para aprender también a obtener el diagrama de bloques del sistema, o la representación en variables de estado. Solicitar vía email – WhatsApp. Se facilita pago por PayPal, Tarjeta de crédito o débito. Costo por toda la guía: 21.5 €. Costo por un ejercicio: 12.5 €.

A continuación, los enunciados de problemas resueltos en esta guía.

1. Hallar la función de transferencia Θ_(s)/T_(s) del Sistema mostrado en la Figura 22.

2. Hallar la función de transferencia Θ_(s)/T_(s) del Sistema mostrado en la Figura 23.

3. Hallar las funciones de transferencia Θ_1(s)/T_(s)  y Θ_2(s)/T_(s)  del Sistema mostrado en la Figura 24._{El mismo ejercicio se resolverá en el próximo número mediante variables de estado.}

4. Hallar la representación en espacios de estados del Sistema del ejercicio anterior, Figura 24, considerando a Θ_1(t) como la salida y a T_(t) como la entrada. Hallar el diagrama de bloques del sistema y a partir de allí la función de transferencia Θ_1(s)/T_(s).

5. Hallar la función de transferencia Θ_L(s)/T_m(s)  del Sistema Motor-Eje Flexible-Carga mostrado en la Figura 26.

6. Hallar las funciones de transferencia Θ_1(s)/T_m(s) y Θ_2(s)/T_m(s)  del Sistema mostrado en la Figura 27.

7. Hallar las funciones de transferencia Θ_1(s)/T_(s) y Θ_2(s)/T_(s)  del Sistema mostrado en la Figura 28.

8. Hallar la función de transferencia Θ_2(s)/T_(s) del Sistema mostrado en la Figura 29.

9. Hallar las funciones de transferencia Θ_1(s)/T_(s) y Θ_2(s)/T_(s)  del Sistema mostrado en la Figura 30. Considerar k₁=9, k₂=3 N-m/rad, b₁=8, b₂=1 N-m-s/rad, J₁=5, J₂=3 Kg-m². _{El mismo ejercicio se resolverá en el próximo número mediante variables de estado.}

10. Hallar la representación en espacios de estados del Sistema del ejercicio anterior, Figura 30, considerando a Θ_2(t) como la salida y a T_(t) como la entrada. Hallar la función de transferencia Θ_2(s)/T_(s), directamente desde la representación en variables de estado obtenida. Considerar k₁=9, k₂=3 N-m/rad, b₁=8, b₂=1 N-m-s/rad, J₁=5, J₂=3 Kg-m².

11. Hallar la representación en espacios de estados del Sistema mostrado en la Figura 32, considerando a Θ_2(t) como la salida y a T_(t) como la entrada. Utilizando Matlab, hallar la función de transferencia Θ_2(s)/T_(s) directamente a partir de la representación en variables de estado obtenida. Considerar k₁= k₂=1 N-m/rad, b₁= b₂=1 N-m/rad, J=1 Kg-m².

12. Hallar Las funciones de transferencia Θ_1(s)/T_m(s) y Θ_2(s)/T_m(s)  del Sistema mostrado en la Figura 33.

Contacto a través de:

• WhatsApp: +34 633129287
• dademuchconnection@gmail.com

Te brindo toda la asesoría que necesites!! … Prof. Larry. Se hacen trabajos, ejercicios, clases online, talleres, laboratorios, Academic Paper, Tesis, Monografías.

Resuelvo problemas y ejercicios en dos horas…atención inmediata!!..

Puedes pagar la guía a través del siguiente enlace:

Sistema masa-resorte-amortiguador. Sistema Rotacional. Problemas resueltos. Catálogo 3

Pago por toda la guía (21.5 euros). Una vez pagado, por favor Solicitar vía whatsapp +34633129287. Ten en cuenta la diferencia horaria. Gracias.

21,50 €

Click here to purchase.

Sistema masa-resorte-amortiguador. Sistema Rotacional. Problemas resueltos. Catálogo 3

Pago por un solo ejercicio (12.5 euros). Una vez pagado, por favor Solicitar vía whatsapp +34633129287. Ten en cuenta la diferencia horaria. Gracias.

12,50 €

Haz clic aquí para comprar.

Respuesta de un Sistema Masa-Resorte-Amortiguador con Condiciones Iniciales

La técnica discutida hasta ahora, la aplicación de la Transformada de Laplace para obtener la función de transferencia, ha implicado condiciones iniciales iguales a cero en el sistema. Es por ello que muchos problemas inician con el anuncio de «suponga que el sistema parte del reposo», o, «suponga condiciones iniciales iguales a cero».

En el caso de que las condiciones iniciales de un sistema Masa-Resorte-Amortiguador no sean cero, la aplicación de la transformada de Laplace tiene una variante que hace poco factible encontrar la función de transferencia del sistema. En cambio, podemos obtener una expresión para la salida X(s) tomando en cuenta dichas condiciones iniciales, para luego evaluar un sistema paralelo cuyo comportamiento sea equivalente al sistema que nos interesa. Veamos.

Consideramos el sistema de la Figura 5-30, con m=1 Kg; b= 3 N-s/m; k=2 N/m:

Si las condiciones iniciales no son iguales a cero, debemos obtener primero la ecuación diferencial del este sistema, la cual es:

Suponemos que en el tiempo t=0 la masa es jalada hacia abajo (sentido positivo) tal que posee las siguientes condiciones iniciales: x(0)=0.1 m; x´=0.05 m/s. Tomando en cuenta condiciones iniciales diferentes de cero, la transformada de Laplace  para x’ es sX(s) – x(0), y para x» es s^2X(s) – sx(0) – x'(0). Por tanto, la transformada de Laplace del sistema anterior es:

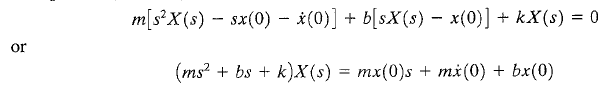
Despejando X(s) obtenemos:

Por tanto, la expresión para la salida considerando las condiciones iniciales diferentes de cero es:

Si aún queremos evaluar el movimiento del sistema mediante una función de transferencia, podemos aplicar una fuerza externa y observar que pasa. Hacemos uso de una de las entradas más comunes para evaluar sistemas: una entrada escalón unitario. Es muy utilizada porque muchos fenómenos se manifiestan de esta manera, cuando la fuerza aparece súbitamente y luego permanece constante.

La ecuación anterior se puede escribir como sigue:

Por lo tanto el movimiento de la masa m puede ser evaluada como la respuesta a la entrada escalón unitario del siguiente sistema cuya Función de Transferencia G(s) es:

Introduzca en el Command Window de Matlab el siguiente código el cual simula el comportamiento del sistema ante una entrada escalón:

> G=tf([0.1 0.35 0],[1 3 2])

>step(G)

> stepinfo(G)

RiseTime: 2.5518

Peak: 0.1042

¿Cómo se puede interpretar este resultado? El sistema originalmente comienza su movimiento en x(0)=0.1 m (offset) y viaja a una velocidad de 0.05 m/s. Según la gráfica, el sistema (la masa m) se desplaza (oscila) levemente hasta 0.1042 m (Peak) al ser «empujada» por una fuerza en forma de escalón unitario en sentido positivo, y en 2.5518 segundos (RiseTime) a regresado a la posición 0,0368 m aprox., que se corresponde con el 63.2%  de su trayecto hasta la posición final que es 0 m, es decir, la masa y el sistema en general regresa desde 0.1 metros a su posición de equilibrio.

Representación en Variables de Estado de un Sistema Masa-Resorte-Amortiguador.

Las variables de estado son la herramienta más poderosa de la Ingeniería de Control Moderna, ya que no está limitada a sistemas lineales como sí o está el método hasta ahora visto, La Transformada de Laplace.

Las variables de estado en el caso del sistema masa-resorte-amortiguador de la Figura 8, nos permitirá reescribir un sistema de segundo orden en un sistema de primer orden. El siguiente material fue obtenido del video: State-Space Representation

                                                                      Figura 8

Seleccionando nuevamente el desplazamiento como la coordenada generalizada, la ecuación de movimiento del sistema es la siguiente:

El objetivo es expresar esta ecuación en una forma equivalente que tiene la siguiente forma:

Aquí el vector es un Vector de Estado, y X1, X2, son variables de estado que sustituyen a la original variable generalizada X y, más importante, a sus derivadas. El describir el sistema en forma de matrix, ofrecerá la enorme ventaja de utilizar el poder de las computadoras para procesar información y ejecutar análisis de datos presentados en forma matricial (Matrix Algebra).

Las ecuaciones encerradas en círculos amarillos muestran como la primera forma de escribir es la forma compacta de escribir las ecuaciones para y.

El primer paso es definir las variables de estado:

Este procedimiento nos permite obtener de inmediato la primera ecuación de estado :

…..por tanto

El segundo paso consiste en forzar al coeficiente que acompaña al orden más alto, el coeficiente líder, a ser igual a la unidad. Para ello, en nuestro caso, se divide la ecuación de movimiento original entre m (y en general, entre el valor que ocupe ese lugar):

En el tercer paso se despeja la derivada de mayor orden:

El cuarto paso consiste en sustituir las derivadas de la variable original por sus ya asignadas variables de estado:

Y así hemos encontrado la segunda ecuación de estado:

….

Y así hemos completado el objetivo. La ecuación de movimiento original puede ser expresado como variables de estado en la siguiente forma:

Ejemplo 2 variables de estado:

Supongamos ahora que tenemos el sistema de la Figura 2.15, para el cual ya habíamos encontrado su Función de Transferencia (ver: Ejemplo 2 – Función Transferencia de sistema masa-resorte-amortiguador):

Debemos encontrar para este sistema su representación en variables de estado.

Para ver todo el resultado ver el siguiente link: Ejemplo 1 – Representación en Variables de Estado de un Sistema Masa-Resorte-Amortiguador

Escrito por: Prof. Larry Obando WhatsApp: +34 633129287 Atención Inmediata!!

SIGUIENTE: Dinámica de una Sistema Electromecánico con Motor DC

Los libros de donde extraje imágenes, ecuaciones e información, son los siguientes:

1. Robert Resnick, tomo1
2. Dinamica_de_Sistemas, Katsuhiko Ogata
3. Control Systems Engineering, Norman Nise
4. Sistemas de Control Automatico, Benjamin Kuo
5. Ingenieria de Control Moderna, 3° ED. – Katsuhiko Ogata
6. Física Tipler 5ta Edición Vol 1
7. SOLUCION TIPLER MOSCA 5TA ED

Catálogos de ejercicios resueltos:

• Sistema masa-resorte-amortiguador. Problemas resueltos. Catálogo 1. 
• Sistema masa-resorte-amortiguador. Problemas resueltos. Catálogo 2. 
• Sistema masa-resorte-amortiguador. Sistema rotacional. Problemas resueltos. Catálogo 3. 
• Sistema masa-resorte-amortiguador con engranajes. Problemas resueltos. Catálogo 4.
• Función de transferencia de sistema eléctrico – Problemas resueltos – Catálogo 5
• Motor DC – Problemas resueltos de sistema electromecánico – Función de Transferencia – Catálogo 6
• Función de transferencia de sistema electrónico – Problemas resueltos – Catálogo 7
• Diagrama de bloques – Problemas resueltos – Sistema MRA – Catálogo 8
• Análisis de respuesta transitoria – Problemas resueltos – Catálogo 9

Atención: Te recomiendo el libro “Sistema masa-resorte-amortiguador, 73 Ejercicios Resueltos”. Lo he escrito luego de agrupar, ordenar y resolver los ejercicios más frecuentes en los libros que se utilizan en las clases universitarias de Ingeniería de Sistemas de Control, Mecánica, Electrónica, Mecatrónica y Electromecánica, entre otras.  Si necesitas adquirir la destreza de solucionar problemas, ésta es una excelente opción para entrenarte y ser eficaz al presentar exámenes, o tener una base sólida para iniciar estas carreras profesionales.  INDICE Capítulo 1———————————————————- 1 Sistema Masa-Resorte-Amortiguador (desplazamiento traslacional) Capítulo 2———————————————————- 51 Sistema Masa-Resorte-Amortiguador (desplazamiento rotacional) Capítulo 3———————————————————- 76 Sistema Mecánico con engranajes Capítulo 4———————————————————- 89 Sistema eléctrico, electrónico Capítulo 5———————————————————-114 Sistema Electromecánico – Motor DC Capítulo 6——————————————————— 144 Sistema del nivel de líquido Capítulo 7——————————————————— 154 Linealización de sistemas no lineales

Sistema masa-resorte-amortiguador, 73 Ejercicios Resueltos

En este libro encontrará ejercicios de sistemas MRA, eléctricos, electrónicos, nivel de líquido, electromecánicos, etc. Su compra incluye una hora de clase online para asesorar sobre el tema o sobre el método utilizado para hallar la función de transferencia de cada sistema. Una vez realizado el pago, por favor enviar copia de recibo de pago al whatsapp +34633129287 para recibir el producto por esa vía. (o por email dademuch@gmail.com en su defecto).

31,70 €

Haz clic aquí para comprar.

Atención: Si lo que Usted necesita es resolver con urgencia un problema:  Atención: Si lo que Usted necesita es determinar La Función de Transferencia de un Sistema..Le entregamos la respuesta en digital. Póngase en contacto con nosotros, respuesta inmediata, resolvemos y entregamos la Función de Transferencia de sistemas masa-resorte-amortiguador, eléctricos, electromecánicos, electromotriz, nivel de líquido, térmico, híbridos, rotacional, no lineales, etc.. Opcional, Representación en Variables de Estado. WhatsApp: +34 633129287, atención inmediata !! email: dademuchconnection@gmail.com

Escrito por Prof. Larry Francis Obando – Technical Specialist – Educational Content Writer – Twitter: @dademuch

Mentoring Académico / Emprendedores / Empresarial

Copywriting, Content Marketing, Tesis, Monografías, Paper Académicos, White Papers (Español – Inglés)

Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV CCs

Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.

Escuela de Turismo de la Universidad Simón Bolívar, Núcleo Litoral.

Contacto: España +34 633129287

Caracas, Valladolid, Quito, Guayaquil, Jaén, Villafranca de Ordizia. 

WhatsApp: +34 633129287

Twitter: @dademuch

FACEBOOK: DademuchConnection

email: dademuchconnection@gmail.com

Relacionado:

Ejemplo 1 – Función Transferencia de Sistema masa-resorte-amortiguador

Ejemplo 2 – Función Transferencia de sistema masa-resorte-amortiguador

Dinámica de una Sistema Electromecánico con Motor DC

Ejemplo 1 – Función de Transferencia de Sistema Electromecánico

Ejemplo 1 – Representación en Variables de Estado de un Sistema Masa-Resorte-Amortiguador

Diagrama de Bloques – Ingeniería de Control

Respuesta Transitoria de un Sistema de Control

Simulación de Respuesta Transitoria con Matlab

Estabilidad de un sistema de control

Error en estado estable de un sistema de control

PID – Acciones básicas de sistemas de control

PID – Efecto de las acciones de control Integral y Derivativo

PID – Diseño y configuración del controlador