Las señales periódicas, exponenciales, escalón unitario y rampa unitaria, son algunas de las funciones del tiempo continuo más utilizadas para el análisis de sistemas en ingeniería.
Una señal x(t) es una función con valor real o escalar de la variable de tiempo t, si para cualquier valor fijo de la variable t, el valor asumido por la señal en ese tiempo t es un número real. Cuando la variable t toma sus valores del conjunto de los números reales, se dice que t es una variable de tiempo continuo, y que la señal x(t) es una señal de tiempo continuo o una señal analógica.
Señales periódicas
Sea T un número real positivo fijo. Se dice que una señal continua x(t) es periódica con período T si se cumple que:
![]()
Si x(t) es periódica con período T, entonces también es periódica con período qT, donde q es cualquier entero positivo. El período fundamental T es el número más pequeño para el cual se cumple la ecuación (1).
La sinusoide es la función periódica por excelencia utilizada en las ciencias y en la ingeniería. Numerosos procesos tienen este comportamiento de manera natural. En la siguiente ecuación sinusoidal, A es la amplitud, ω es la frecuencia en radianes por segundo, y θ es la fase en radianes, aunque también suele expresarse en grados:
![]()
La frecuencia f en Hertz, y el período T en rad/s, de la función en la ecuación(2) son:

La sinusoide de la Figura (1) representa el caso en que:
![]()
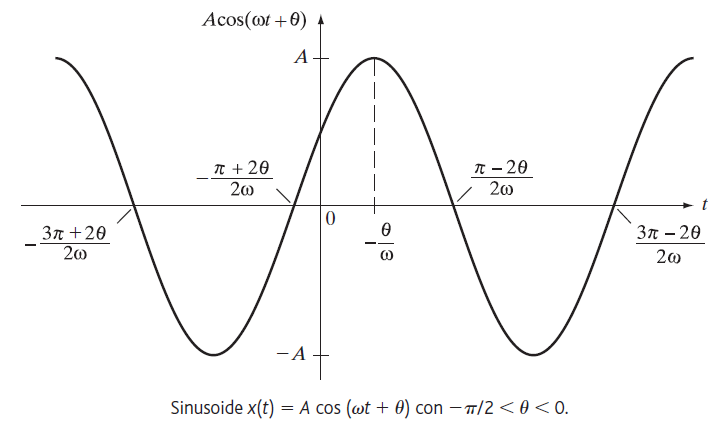
Ejemplo y simulación de la Señal sinusoidal
La sinusoide es la función periódica por excelencia utilizada en las ciencias y en la ingeniería. Numerosos procesos tienen este comportamiento de manera natural. El caso de un circuito eléctrico es de relevante importancia. Los circuitos de corriente alterna tienen voltajes y corrientes sinusoidales. Suponga que se tiene el circuito de la Figura (2):
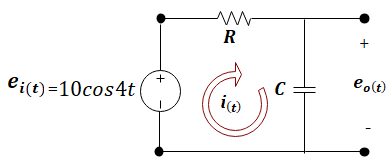
Hemos calculado la corriente y el voltaje en este sistema en el artículo siguiente: La impedancia y la admitancia de un circuito eléctrico. La solución para el voltaje eo(t) es:


Este resultado se puede visualizar a través de una simulación computarizada, introduciendo el siguiente código en Matlab:

El resultado se puede observar en la Figura siguiente:
Señales exponenciales
Las señales exponenciales son extremadamente importantes en el análisis de señales y sistemas, ya que ellas sirven como bloques fundamentales a partir de los cuales podemos construir muchas otras señales.
En la Figura (4) vemos el caso de una función exponencial ascendente y de inmediato se muestra su estructura matemática.

![]()
En la Figura (5) vemos el caso de una función exponencial descendente y de inmediato se muestra su estructura matemática.
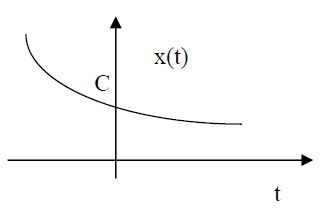
![]()
Ejemplo y simulación de la Señal exponencial
La función exponencial también representa muchos procesos de la naturaleza, como por ejemplo, el crecimiento de una comunidad de bacterias. Es de gran utilidad la función exponencial para representar el caso de movimientos amortiguados en el campo de la mecánica. La Figura (6) muestra la Función de Transferencia para un sistema masa-resorte-amortiguador simple:
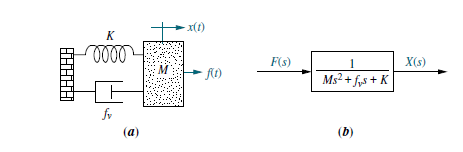
La dinámica del sistema de la Figura (6) se describe mediante una sola ecuación diferencial:

En la ecuación (5), x(t) es el desplazamiento horizontal del sistema, que es un desplazamiento sinusoidal amortiguado, conocido como movimiento armónico amortiguado, concepto básico para la física y la ingeniería mecánica clásica.
La siguiente ecuación es una solución para la ecuación diferencial (5). Se trata de una función exponencial multiplicada por una función sinusoidal:

Con el fin de utilizar el mismo código de Matlab utilizado en el ejemplo de la función sinusoidal, supongamos el siguiente ejemplo para la ecuación anterior de x(t):
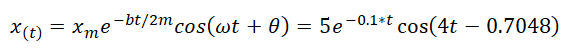
Este resultado se puede visualizar a través de una simulación computarizada, introduciendo el siguiente código en Matlab:
>> t=0:0.01:30;
>> x=5*exp(-0.1*t).*cos(4*t-0.7048);
>> plot(t,x)
>> grid
>> xlabel(‘Tiempo(segundos)’)
>> ylabel(‘Desplazamiento X(metros)’)

En la siguiente Figura vemos remarcada la influencia de la función exponencial de color naranja, denominada «envolvente»:
>> t=0:0.01:30;
>> x=5*exp(-0.1*t).*cos(4*t-0.7048);
>> y=5*exp(-0.1*t);
>> plot(t,x,t,y)

Para mayor información en este tema ver: Ejercicio de dinámica masa-resorte-amortiguado, función de transferencia.
Funciones escalón y rampa
Dos señales ampliamente utilizadas en el campo de la ingeniería son el escalón unitario u(t) y la función rampa unitaria r(t), mostradas en la Figura 9:

En particular, para el análisis de sistemas, estas funciones son ideales. A veces es posible predecir el comportamiento de tales sistemas, o el tipo de entrada que tendrán que procesar con mayor frecuencia. Si se prevé que la entrada a un sistema será un cambio instantáneo, como por ejemplo una entrada al sistema de suspensión de un automóvil, lo más razonable es probar ese sistema con una entrada escalón unitario (step). Si por el contrario, esa entrada cambia proporcionalmente con el tiempo, el sistema debe probarse con una entrada rampa unitaria.
Ejemplo y simulación de la Señal Escalón Unitario
Ambas señales, escalón unitario y rampa unitaria, son ampliamente utilizadas en sistemas de control, porque permiten visualizar la respuesta transitoria del sistema y el error en estado estable.
Suponga que se solicita determinar la respuesta transitoria a una entrada escalón unitario, del siguiente Sistema mecánico rotacional:

Dónde:

Se sabe que la función de transferencia del sistema es la siguiente:

Determinar la respuesta transitoria implica determinar el valor de los siguientes parámetros:
- Sobrepaso máximo, tiempo de levantamiento, tiempo de asentamiento, entre otros.
En Matlab, podemos responder esta pregunta mediante el siguiente comando:
>> numg=1/J;
>> deng=[1 D/J K/J];
>> G=tf(numg,deng)
G =
3.846
—————–
s^2 + 4 s + 19.23
>> stepinfo(G)
RiseTime (tiempo de levantamiento): 0.3554 s
SettlingTime (tiempo de asentamiento): 1.8989 s
Overshoot (Sobrepaso máximo): 19.9891 %
Peak: 0.2400
El analista obtiene una excelente representación gráfica de esta respuesta mediante:
>> step(G)

El diagrama siguiente esquema muestra lo que hemos hecho. Hemos colocado una función escalón unitario en la entrada del sistema que tiene la función de transferencia G(s) y hemos obtenido la respuesta mostrada a la salida:

Para más información en este tema ver: Respuesta Transitoria de un Sistema de Control
Fuentes:
- Fundamentos_de_Señales_y_Sistemas_usando la Web y Matlab
- Análisis de sistemas lineales asistido con Scilab, Ebert Brea.
- Analisis_de_Sistemas_Lineales
- Oppenheim – Señales y Sistemas
- Señales y circuitos lineales
Escrito por Prof. Larry Francis Obando – Technical Specialist – Educational Content Writer – Twitter: @dademuch
Se hacen trabajos, se resuelven ejercicios!!
WhatsApp: +34633129287 Atención Inmediata!!
Mentoring Académico / Emprendedores / Empresarial
Copywriting, Content Marketing, Tesis, Monografías, Paper Académicos, White Papers (Español – Inglés)
Escuela de Ingeniería Electrónica de la Universidad Simón Bolívar, USB Valle de Sartenejas.
Escuela de Ingeniería Eléctrica de la Universidad Central de Venezuela, UCV Caracas.
Escuela de Turismo de la Universidad Simón Bolívar, Núcleo Litoral.
Contacto: España. +34633129287
Caracas, Quito, Guayaquil, Jaén.
WhatsApp: +34633129287
FACEBOOK: DademuchConnection
email: dademuchconnection@gmail.com

1 comentario en “Señales elementales en el tiempo continuo – Ejemplos y Simulación en Matlab”